Nie znam całego rozwiązania, ale mogę pokazać ci drogę, którą prawdopodobnie możesz przejść.

Jak @nluigi zauważył w swoim komentarzu, równania rządzące twoim problemem są podane w Modelowanie przejściowego przenikania ciepła między dwoma materiałami 1-D:

$$ \ frac {\ Part T} {\ Part t} = \ alpha \ frac {\ Part ^ 2 T} {\ częściowe x ^ 2} $$

z temperaturą $ T $, dyfuzyjnością cieplną $ \ alpha = \ frac {k} {\ rho \, c_P} $, time $ t $, space $ x $, przewodnictwo cieplne $ k $, gęstość $ \ rho $ i ciepło właściwe $ c_P $.

Podstawowym rozwiązaniem tego równania różniczkowego jest

$$ H (x , t) = \ frac {1} {(4 \ pi \ alpha t) ^ {\ frac {n} {2}}} \, \ exp \ left (- \ frac {| x | ^ 2} {4 \ alpha t} \ right) $$

gdzie $ n $ jest wymiarem współrzędnej przestrzeni $ x $ i $ | x | ^ 2 = \ sum_ {i = 1} ^ n x_i ^ 2 $ jest kwadratem normy Euklidów (gdzie $ x_i $ to współrzędne $ x $ w układzie współrzędnych kartezjańskich). Należy zauważyć, że $ x $ może być wartością skalarną dla problemów jednowymiarowych ($ n = 1 $), dwuwymiarowym wektorem dla problemów dwuwymiarowych ($ n = 2 $) lub trójwymiarowym wektorem dla trójwymiarowych problemy wymiarowe ($ n = 3 $).

Przykładem problemu jednowymiarowego jest przenoszenie ciepła przez ścianę. Twój problem jest (w przybliżeniu) dwuwymiarowy. Trójwymiarowym problemem byłaby gorąca lub zimna kula w dużym pomieszczeniu.

Aby obliczyć rozwiązanie konkretnego problemu, potrzebujesz warunków początkowych, podanych jako

$$ T (x, t = 0) = T_0 (x) $$

i obliczyć splot między rozwiązaniem podstawowym a warunkami początkowymi:

$$ T (x, t) = (H * T_0) (x, t) = \ int \ limits _ {{\ mathbb R} ^ n} H (xy, t) \, T_0 (y) \, \ mathrm {d} y \\ T (x, t) = \ frac {1} {(4 \ pi \ alpha t) ^ {\ frac {n} {2}}} \ int \ limits _ {{\ mathbb R} ^ n} \ exp \ left (- \ frac {| xy | ^ 2} {4 \ alpha t} \ right) T_0 (y) \, \ mathrm {d} y $$

Kiedy dobrze zrozumiem Twój problem, możesz użyć

$$ T_0 (x) = \ left \ {\ begin {array} {ll} T_I & \ mbox {for} | x | < x_B \\ 0 & \ mbox {w przeciwnym razie} \ end {array} \ right. $$

gdzie $ T_I $ to temperatura wewnętrzna na początku, a $ x_B $ to współrzędna ściany. Zauważ, że ponieważ równanie różniczkowe jest liniowe, możesz dodać do roztworu dowolną temperaturę bazową, a także pomnożyć rozwiązanie w dowolnej skali. Tak więc ze względu na matematyczne rozwiązanie można obliczyć z $ T_I = 1 $ i wyskalować wynik. Jednak jestem inżynierem i nie zaszkodzi po prostu przeciągnąć $ T_I $ razem.

Niedawno miałem problem jednowymiarowy, a ten nadal można rozwiązać z pewnym wysiłkiem:

$$ T (x, t) = \ frac {1} {\ sqrt {4 \ pi \ alpha t}} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ exp \ left (- \ frac {| xy | ^ 2} {4 \ alpha t} \ right) T_0 (y) \, \ mathrm {d} y \\ = \ frac {T_I} {\ sqrt {4 \ pi \ alpha t}} \ int \ limits _ {- x_B} ^ {+ x_B} \ exp \ left (- \ frac {| xy | ^ 2} {4 \ alpha t} \ right) \, \ mathrm {d} y \\ = \ frac {T_I} {2} \ left (\ mathrm {erf} \ left (\ frac {x + x_B} {\ sqrt {4 \ alpha t}} \ right) - \ mathrm {erf} \ left (\ frac {x-x_B} {\ sqrt {4 \ alpha t}} \ right) \ right) $$

z $ \ mathrm {erf} (x) = \ frac {2} {\ sqrt {\ pi}} \ int \ limits_0 ^ x \ exp \ left (-t ^ 2 \ right) \, \ mathrm {d} t $ jest funkcją błędu.

Dla $ \ alpha = 1 $, $ T_I = 1 $, $ x_B = 1 $ Poniższy wykres przedstawia rozwiązanie dla niektórych $ t $:

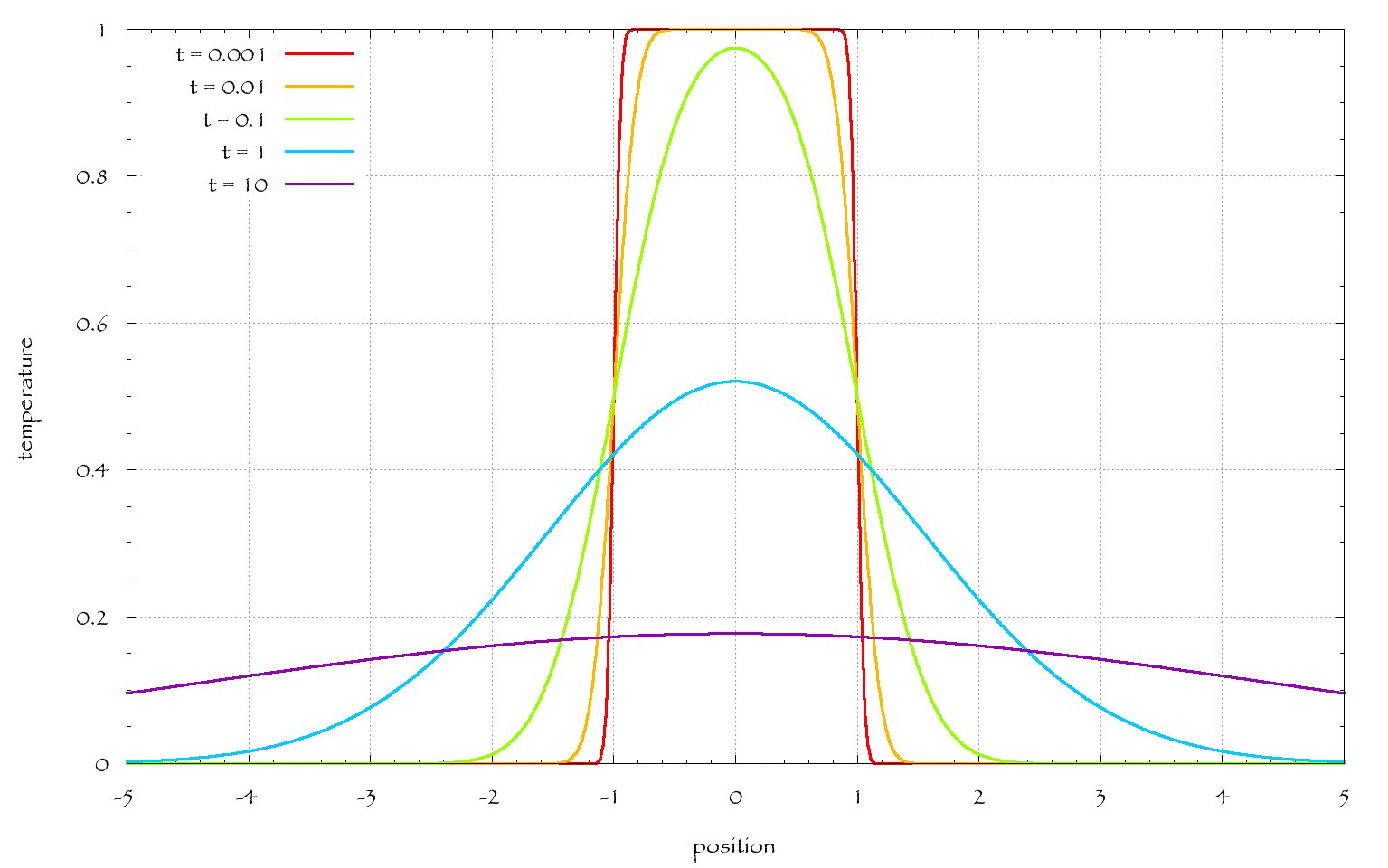
Jednak dla wyższych wymiarów warunków początkowych podanych powyżej równanie należy przekształcić na sferyczne współrzędne jod t. W przypadku dwóch wymiarów otrzymujesz

$$ T (x, t) = \ frac {1} {4 \ pi \ alpha t} \ int \ limits _ {{\ mathbb R} ^ 2} \ exp \ left (- \ frac {| xy | ^ 2} {4 \ alpha t} \ right) T_0 (y) \, \ mathrm {d} y \\\ Rightarrow \ quadT (x, t) = \ frac {T_I} {4 \ pi \ alpha t} \ int \ limits_ {0} ^ {r_B} \ left (\ int \ limits_0 ^ {2 \ pi} \ exp \ left (- \ frac {| xy | ^ 2} {4 \ alpha t} \ right) \, \ mathrm {d} \ varphi (y) \ right) r (y) \, \ mathrm {d} r (y) $$

dając (przynajmniej ja ) znaczne bóle głowy podczas próby oceny. Prawdopodobnie ktoś tam wie, co

$$ \ int \ limits_0 ^ {2 \ pi} \ exp \ left (- | xy | ^ 2 \ right) \, \ mathrm {d} \ varphi (y ) $$

ocenia, ale obecnie nie. Prawdopodobnie istnieje również znacznie czystsze podejście do oceny całki splotowej w dwóch wymiarach.